k-means++: The Advantages of Careful Seeding

Introduction

This post will discuss and re-implement the $k$-means++ algorithm proposed by Arthur and Vassilvitskii (2007)¹. By understanding the algorithm, we may be able to integrate it with the clusterwise linear regression problem and measure its performance against existing methods.

If you have used the scikit-learn library to perform $k$-means clustering then most likely you have used the k-means++ algorithm to initialise the centroids. You get two options for initialisation:

1. Randomly select $k$ points from the dataset as the initial centroids.
2. Use the k-means++ algorithm to select the initial centroids.

For example:

from sklearn.cluster import KMeans

option1 = KMeans(n_clusters=3, init='k-means++')
option2 = KMeans(n_clusters=3, init='random')

If you don’t specificy the init method, you will use the k-means++ algorithm by default.

We want to understand what this algorithm is doing from the ground up to build better intuition for it. In practice, however, we’d use scikit-learn’s implementation since it’s well tested and significantly more efficient than our own would be.

The Lloyd Algorithm

Arthur and Vassilvitskii start by introducing the Lloyd algorithm which was proposed in 1957 but only officially published in 1982².

The algorithm is a local search method that begins by selecting $k$ starting points from the dataset at random. Each point from the dataset is then:

1. Assigned to the nearest $k$ center, and then
2. Each $k$ center is recomputed as the center of mass of all points assigned to it.
3. Do step 1 and 2 until the objective function converges.

The wikipedia page for the Lloyd algorithm has a nice visualisation of the algorithm using a Voronoi diagram, which I have added below.

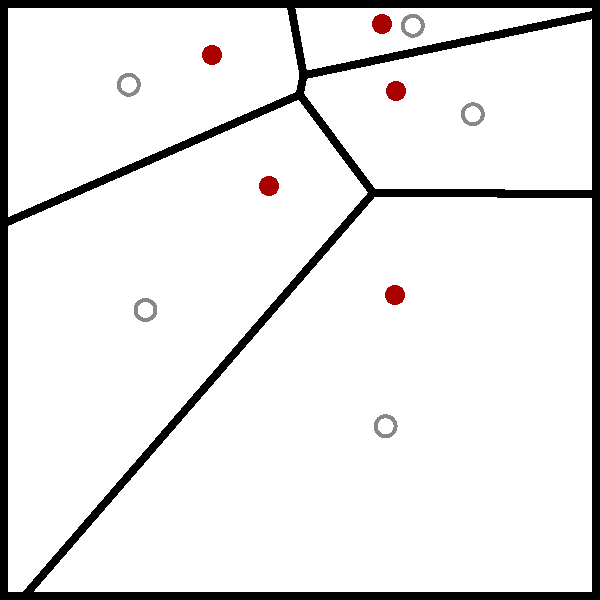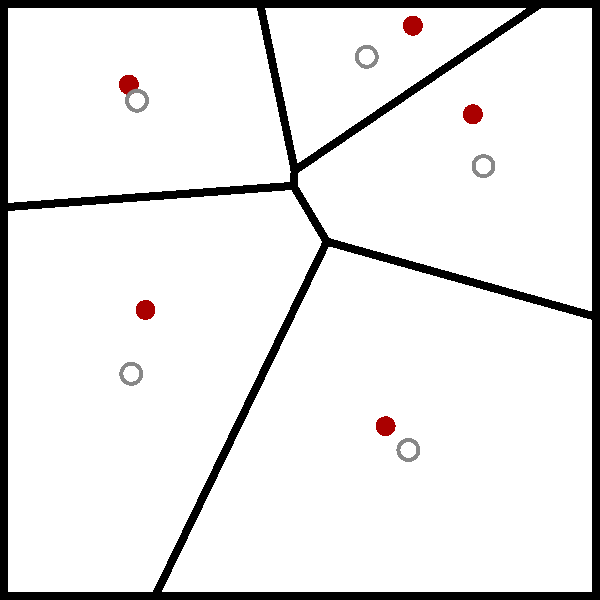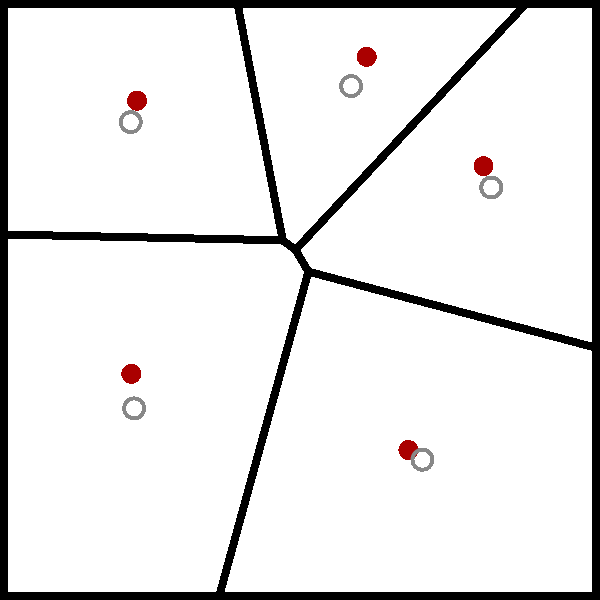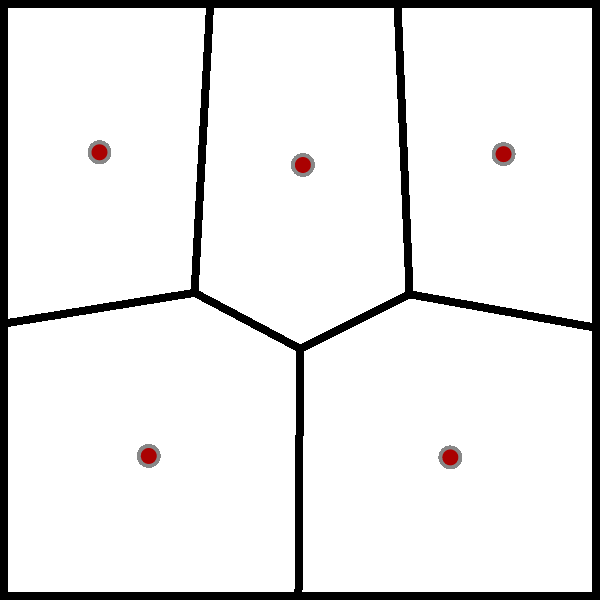
While I have heard of the Lloyd algorithm before, I have never really took the time to understand it. But now that I have, it is clear that the Lloyd algorithm is just the standard implementation of the $k$-means algorithm.

We will refer to the Lloyd algorithm as the $k$-means algorithm for the rest of this post.

Motivation for $k$-means++

Arthur and Vassilvitskii point out that while the $k$-means algorithm is very efficient, it can produce arbitrarily bad clusterings. More specifically, they state that the approximation ratio of $\frac{\phi}{\phi_{OPT}}$ is unbounded even when $n$ and $k$ are fixed.

The key problem is due to random initialisation, since $k$-means is a local search algorithm, and greedily accepts improvements, it is possible to get stuck in a local minimum from globally bad starting points.

Due to the limitation of finding initial starting points, Arthur and Vassilvitskii propose a new algorithm, $k$-means++, which in fact still chooses $k$ centers randomly but with very specific probabilities.

In particular, they state:

…we choose a point $p$ as a center with probability proportional to $p$’s contribution to the overall potential. Letting $\phi$ denote the potential after choosing centers in this way, we show the following.

Theorem 1.1. For any set of data points, $E[\phi] \leq 8(\ln k+2)\phi_{OPT}$

There are two parts here, which are preliminarily important to understand. First, choosing starting points with probability proportional to their contribution to the overall potential means the points that are chosen are likely to be spread out across our problem space.

The second is the statement of the theorem which states that on average, the total potential is less than or equal to $8(\ln k+2)$ times the optimal potential.

We will go into more detail on the theorem in the next section.

Preliminaries

In this discussion we will skip a lot detail around the $k$-means clustering problem and focus more on the k-means++ algorithm and other related algorithms in the paper. For more details on the $k$-means clustering problem, you can read about it in my previous blog post on the modified global $k$-means algorithm.

I do however want to state the problem formulation for the $k$-means clustering problem (exactly how the authors formulate it). This is only because it will be useful to have in mind when we discuss the k-means++ algorithm.

Given $k \in \mathbb{N}$ and a set of $n$ points in $\mathbb{R}^d$, our objective is to choose $k$ centers $\{c_1, c_2, \ldots, c_k\} \subset \mathbb{R}^d$ to minimise the following potential function:

$$\begin{align*} \phi = \sum_{x \in \mathcal{X}} \min_{c \in \mathcal{C}} \left\| x - c \right\|^2 \end{align*}$$

Note that the potential is in fact the objective function we want to minimise, I am using the same terminology as the authors to avoid confusion as I read through the paper.

The code to this objective function is:

def phi(X, C):
    error = 0
    for x in X:
        min_dist = np.inf
        for c in C:
            dist = np.sum((x - c)**2)
            if dist < min_dist:
                min_dist = dist
        error += min_dist
    return error

The optimal clustering for the problem is denoted as $\mathcal{C}_{OPT}$ and is the clustering that minimises the potential function to the minimum possible value which is $\phi_{OPT}$.

Another important notation noted in the paper is:

Given a clustering $\mathcal{C}$ with potential $\phi$, we also let $\phi(\mathcal{A})$ denote the contribution of $\mathcal{A} \subset \mathcal{X}$ to the potential..

Where $\phi(\mathcal{A})$ is given by:

$$\begin{align*} \phi(\mathcal{A}) = \sum_{x \in \mathcal{A}} \min_{c \in \mathcal{C}} \left\| x - c \right\|^2 \end{align*}$$

This is the potential of the points in $\mathcal{A}$ given the clustering $\mathcal{C}$.

Problem Dataset

We will use the make_blobs function from scikit-learn to generate a dataset to use throughout this post. In particular, we will generate a dataset with $k=5$ clusters and $n=100$ points then store it in $\mathcal{X}$.

k = 5
n = 100

X, _ = make_blobs(
    n_samples=n,
    cluster_std=0.5,
    centers=k,
    n_features=2,
    random_state=1,
)

If we plot the generated dataset, we get the following:

This is a dataset with 5 obvious clusters and is a simple benchmark dataset to use for sense checking our re-implementations of the $k$-means algorithm.

$k$-means Algorithm

The traditional implementation of the $k$-means algorithm is as follows:

Step 1: We choose $k$ initial centers $\mathcal{C} = \{c_1, c_2, \ldots, c_k\}$ from the dataset at random.

This is written in code as:

def init_c(X, n, k):
    return X[np.random.randint(0, n, size=k)]

If we run this initialisation 100 times, this is what we get:

Step 2: Then for each $i \in \{1, 2, \ldots, k\}$, we assign the cluster $\mathcal{C}_i$ to the points in $\mathcal{X}$ that are nearest to $\mathcal{c}_i$ than $\mathcal{c}_j$ for all $j \in \{1, 2, \ldots, k\}$ and $j \neq i$.

Which looks like the following:

def update_w(X, C, n, k):
    w = np.zeros((n, k))
    for i in range(n):
        d = [np.sum((C[j] - X[i]) ** 2) for j in range(k)]
        nearest_center = np.argmin(d)
        w[i, nearest_center] = 1
    return w

If we take a random initialisation and plot the clusters, we get the following:

Because we are choosing initial centers at random, we are as likely to find points that are directly next to each other as we are to find points that are far away.

The next step, doing step 2 i.e. the assignment step:

w = update_w(X, C, n, k)

We might expect to get the following:

Step 3: After the assignment step, we want to recompute the ceneters such that for each $i \in \{1, 2, \ldots, k\}$ set $c_i$ to be the center of mass of all points assigned to it.

In code this would look like:

def update_c(w, X):
    d = w.sum(axis=0).reshape(-1, 1)
    if np.any(d == 0):
        res = np.zeros_like(w.T @ X)
        mask = d != 0
        m_flat = mask.flatten()
        res[m_flat] = (w.T @ X)[m_flat] / d[mask]
        return res
    else:
        return w.T @ X / d

I don’t show the output of this step here but imagine that for each of our assigned clusters, we take the mean of the points in that cluster and set that as the new center.

Step 4: We repeat steps 2 and 3 until $\mathcal{C}$ no longer changes.

We can put this all together which will give us the following:

def lloyd_algorithm(X, C, n, k, max_iters=100):
    C_current = C.copy()
    for _ in range(max_iters):
        w = update_w(X, C_current, n, k)
        C_current = update_c(w, X)
    return C_current, w

This is the standard implementation of the $k$-means algorithm and is the same implementation I used in my previous blog post but changed the naming convention to match the paper.

Why use the center of mass?

One thing I want to point out from the paper which I found interesting and worth knowing (may be obvious to some) but the authors state that:

To see that Step 3 does in fact decreases $\phi$, it is helpful to recall a standard result from linear algebra.

They state this in Lemma 2.1.

Let $S$ be a set of points with center of mass $c(S)$, and let $z$ be an arbitrary point. Then, $$\begin{align*} \sum_{x \in S} \|x - z\|^2 - \sum_{x \in S} \|x - c(S)\|^2 = |S| \cdot \|c(S) - z\|^2 \end{align*}$$

We can rewrite this so the notation is more familiar to what we have been discussing so far. While we don’t need to prove this, it is useful to understand how the lemma was derived.

Consider a cluster $\mathcal{C}_i$ which is the set of points assigned to center $c_i$ with center of mass $\bar{c}_i$, and let $c_i$ be the current center.

We want to show that:

$$\begin{align*} \sum_{x \in \mathcal{C}_i} \|x - c_i\|^2 - \sum_{x \in \mathcal{C}_i} \|x - \bar{c}_i\|^2 = |\mathcal{C}_i| \cdot \|\bar{c}_i - c_i\|^2 \end{align*}$$

Starting with only the first term, for any point $x \in \mathcal{C}_i$ we may write:

$$\begin{align*} \|x - c_i\|^2 &= \|(x - \bar{c}_i) + (\bar{c}_i - c_i)\|^2 \\ &= \|x - \bar{c}_i\|^2 + \|\bar{c}_i - c_i\|^2 + 2\langle x - \bar{c}_i, \bar{c}_i - c_i \rangle \end{align*}$$

Which means that the first term is:

$$\begin{align*} \sum_{x \in \mathcal{C}_i} \|x - c_i\|^2 &= \sum_{x \in \mathcal{C}_i} \|x - \bar{c}_i\|^2 + \sum_{x \in \mathcal{C}_i} \|\bar{c}_i - c_i\|^2 + 2\sum_{x \in \mathcal{C}_i} \langle x - \bar{c}_i, \bar{c}_i - c_i \rangle \end{align*}$$

Investigating the first two terms, we have:

$$\begin{align*} \sum_{x \in \mathcal{C}_i} \|x - \bar{c}_i\|^2 &= \text{ Total variance around the center of mass } \bar{c}_i \\ \sum_{x \in \mathcal{C}_i} \|\bar{c}_i - c_i\|^2 &= |\mathcal{C}_i| \cdot \|\bar{c}_i - c_i\|^2 \\ \end{align*}$$

For the third term, we have:

$$\begin{align*} 2\sum_{x \in \mathcal{C}_i} \langle x - \bar{c}_i, \bar{c}_i - c_i \rangle &= 2 \langle \sum_{x \in \mathcal{C}_i}(x - \bar{c}_i), \bar{c}_i - c_i \rangle \\ &= 2 \langle 0, \bar{c}_i - c_i \rangle \\ &= 0 \end{align*}$$

This means that:

$$\begin{align*} \sum_{x \in \mathcal{C}_i} \|x - c_i\|^2 &= \sum_{x \in \mathcal{C}_i} \|x - \bar{c}_i\|^2 + |\mathcal{C}_i| \cdot \|\bar{c}_i - c_i\|^2 \\ \sum_{x \in \mathcal{C}_i} \|x - c_i\|^2 - \sum_{x \in \mathcal{C}_i} \|x - \bar{c}_i\|^2 &= |\mathcal{C}_i| \cdot \|\bar{c}_i - c_i\|^2 \end{align*}$$

Which proves the center of mass $\bar{c}_i$ always gives the minimum sum of squared distances for any point $x \in \mathcal{C}_i$.

Understanding $k$-means++

I was fascinated by how simple this algorithm is to implement, which makes it even more impressive that it has been a state-of-the-art method for finding starting points for $k$-means clustering since 2007.

We still apply random initialisation, but instead of choosing points with equal probability from a uniform distribution, we now weight the probabilities based on squared distances to existing centers. In particular, the probability distribution is given by:

$$\begin{align*} \text{Sample } x' \in \mathcal{X} \text{ with probability } P(x') = \frac{D(x')^2}{\sum_{x \in \mathcal{X}} D(x)^2} \end{align*}$$

Where $D(x)$ is the shortest distance from a data point $x$ to the closest center.

Step 1: We choose the first center $c_1$ from the dataset at random.

C = np.zeros((k, 2))
C[0] = X[np.random.choice(len(X))]

Step 2/3: Set $c_i = x' \in \mathcal{X}$ using the probability distribution given by $P(x')$.

for i in range(1, k):
    D = []
    for x in X:
        min_dist = np.inf
        for c in C[:i]:
            d = np.sum((x - c) ** 2)
            if d < min_dist:
                min_dist = d
        D.append(min_dist)

    D = np.array(D)
    p = D / np.sum(D)
    C[i] = X[np.random.choice(len(X), p=p)]

The third part of this step is to run step 2 until we have $k$ starting points.

Step 4: Run $k$-means with the starting points $\mathcal{C}$ from step 2/3.

C, _ = lloyd_algorithm(X, C, n, k, max_iters=100)

The full initialisation code is:

def kmeans_pp(X, k):
    C = np.zeros((k, X.shape[1]))
    C[0] = X[np.random.choice(len(X))]

    for i in range(1, k):
        D = []
        for x in X:
            min_dist = np.inf
            for c in C[:i]:
                d = np.sum((x - c) ** 2)
                if d < min_dist:
                    min_dist = d
            D.append(min_dist)

        D = np.array(D)
        p = D / np.sum(D)
        C[i] = X[np.random.choice(len(X), p=p)]

    return C

Initial Intuition

There is a lot more detail to cover on the why but we will discuss this eventually. However, for now, I want to establish some basic intuition for why this probability distribution leads to better starting points.

We first randomly choose a point from the dataset to start with.

c1 = X[np.random.choice(len(X))]

Now $c_1$ is our first center and is chosen uniformly at random, meaning that the probability of choosing any point is $\frac{1}{n}$ where $n$ is the number of points in the dataset. All this means is that every point has an equal chance of being chosen as the first center.

If we want we can visualise where the first center is chosen from the dataset:

Now we already know the issue with using random initialisation is that we are as likely to get a point directly next to our first center as we are to get a point that is far away.

Acknowledging this limitation, Arthur and Vassilvitskii proposed to use a probability distribution that is proportional to the squared distance to the nearest center rather than a uniform distribution.

Now given we have chosen $c_1$, we can generate the probability distribution which we will use to sample the next center.

D = []
for x in X:
    d = np.sum((x - c1) ** 2)
    D.append(d)

D = np.array(D)
p = D / np.sum(D)

For this case since we are only doing an example up to $k=2$, I have simplified the code to just calculate the squared distance to the first center.

If we plot the probabilities of selecting each point, we get the following:

How we interpret this plot is that the points are coloured based on the probability of being chosen as the second center. The darker the blue, the more likely the point is to be chosen as the second center.

If we now use this distribution to sample the second center:

c2 = X[np.random.choice(len(X), p=p)]

and plot it, we get the following:

Because we are more likely to choose points that are further from any existing center, we avoid clustering our initial centers together and get much better starting points for the $k$-means algorithm.

Why is this better?

This section of the post is going to be decomposing a lot of the mathematics from the paper into code to understand how this all works computationally.

Lemma 3.1.

The authors state that:

$k$-means++ is $\mathcal{O}(\log k)$-competitive.

and provide Theorem 3.1. which is:

If $\mathcal{C}$ is constructed with $k$-means++ then the corresponding potential function $\phi$ satisfies $E[\phi] \leq 8(\ln k+2)\phi_{OPT}$.

Recall that $k$-means with random initialisation could be arbitrarily bad, but now with $k$-means++ we have an approximate bound, which means even in the worst case we are bounded by a constant factor of the optimal potential.

The authors then provide another lemma which states:

Let $A$ be an arbitrary cluster in $\mathcal{C}_{OPT}$, and let $\mathcal{C}$ be the clustering with just one center, which is chosen uniformly at random from $A$.

Then, $E[\phi(A)] = 2\phi_{OPT}(A)$.

The nice thing about this lemma is that we can show it computationally. First, we want to rewrite the potential function so that we are computing the potential only for a single cluster.

_phi = lambda X, C: np.sum(np.linalg.norm(X - C, axis=1) ** 2)

Then we can set up a dataset at random:

rows = np.random.randint(10, 100)
cols = np.random.randint(1, 10)

A = np.random.rand(rows, cols)

Previously we showed that the center of mass is the point that minimises the sum of squared distances for any point in the cluster. This means that $\phi_{OPT}(A)$ is going to be the mean of $A$ and we can compute this as:

c = np.mean(A, axis=0)

Then for the final step, we need to show that the expected value of the potential function is twice the optimal potential. Which we can do by running the following code:

E = 0
for i in range(len(A)):
    E += _phi(A, A[i])

print(np.allclose(E / len(A), 2 * _phi(A, c)))

True

This confirms that the expected value of the potential function is twice the optimal potential. However, we only showed this computationlly and to understand how this bound was derived, please refer to the paper.

Lemma 3.2.

The next is analagous to lemma 3.1. but for the remaining centers:

Let $A$ be an arbitrary cluster in $\mathcal{C}_{OPT}$, and let $\mathcal{C}$ be an arbitrary clustering.

If we add a random center to $\mathcal{C}$ from $A$, chosen with $\mathcal{D}^2$ weighting, then $E[\phi(A)] \leq 8\phi_{OPT}(A)$.

The authors show that while $k$-means++ makes probabilistic choices for centers, the triangle inequality limits how bad these choices can be, and in the worst case, the expected potential for any cluster is only a factor of 8 worse than optimal.

Like we did with with lemma 3.1. we can show this computationally. This time since we are dealing with multiple centers, I am going to generate a dataset using make_blobs from scikit-learn.

Using the generated dataset, we can now show this holds for 10,000,000 trials.

CHECK = []
ratios = []

for _ in range(10_000_000):
    X, C = make_blobs(
        n_samples=100,
        centers=3,
        cluster_std=1.0,
        n_features=2,
        random_state=None,
    )

    A = X[C == 0]
    Z = [X[np.random.choice(len(X))] for _ in range(2)]
    opt_c = np.mean(A, axis=0)

    D = [compute_d(a, Z) for a in A]
    E = 0
    for i, a0 in enumerate(A):
        P_a0 = D[i] ** 2 / sum(d**2 for d in D)
        E += P_a0 * _phi(A, np.array([[a0]]))

    ratios.append(E / _phi(A, opt_c))

print(f"E ratio: {np.mean(ratios):.2f}")
print(f"Max ratio observed: {max(ratios):.2f}")
print(f"Individual violations: {sum(1 for r in ratios if r > 8)}")
print(f"E value <= 8? {np.mean(ratios) <= 8}")

E ratio: 2.36
Max ratio observed: 8.88
Individual violations: 1
E value <= 8? True

From this computational experiment, we find that across 10,000,000 trials, the expected ratio converges to 2.36, which is well below the guaranteed bound of 8.

We found only one trial where the ratio reached 8.88, which doesn’t violate the bound, as it guarantees that the expected value remains bounded, not that every individual ratio is bounded.

All this means that if $k$-means++ picks centers such that each of the $k$ optimal clusters contributes at least one center, then we are guaranteed to be bounded by a factor of 8.

For example, if we consider the following:

On the left we see random k-means initialisation with poor cluster coverage and on the right we see $k$-means++ with $D^2$ weighting achieving better coverage of optimal clusters, satisfying Lemma 3.2’s assumption.

Note: Both methods are random - $k$-means++ doesn’t guarantee coverage nor does random initialisation prevent it. $D^2$ weighting simply makes coverage more probable. This example shows where Lemma 3.2’s assumption holds.

Lemma 3.3.

The next lemma 3.3 shows that the total error in general is at most $\mathcal{O}(\log k)$ which the authors prove using induction.

The authors state that:

Let $\mathcal{C}$ be an arbitrary clustering. Choose $u > 0$ “uncovered” clusters from $\mathcal{C}_{OPT}$, and let $\mathcal{X}_u$ denote the set of points in these clusters.

Also let $\mathcal{X}_c = \mathcal{X} - \mathcal{X}_u$.

Now suppose we add $t \leq u$ random centers to $\mathcal{C}$, chosen with $\mathcal{D}^2$ weighting.

Let $\mathcal{C}'$ denote the resulting clustering and let $\phi'$ denote the corresponding potential. Then, $E[\phi']$ is at most:

$$\begin{align*} \left(\phi(X_c) + 8\phi_{OPT}(X_u)\right) \cdot (1 + H_t) + \frac{u - t}{u} \cdot \phi(X_u) \end{align*}$$

The authors define the harmonic sum as: $$\begin{align*} H_t = 1 + \frac{1}{2} + \cdots + \frac{1}{t} \end{align*}$$

To best explain the authors proof (included in the paper for lemma 3.3) we can consider a working example.

Let’s say we have the following clustering problem:

Base Case 1:

We have $t=0$ and $u > 0$ which means we have no covered clusters and some number of uncovered clusters.

This results in the following:

$$\begin{align*} E[\phi'] &\leq \left(\phi(X_{c}) + 8\phi_{OPT}(X_u)\right) \cdot (1 + H_0) + \frac{u - 0}{u} \cdot \phi(X_u) \\ &\leq \left(0 + 8\phi_{OPT}(X_u)\right) \cdot 1 + 1 \cdot \phi(X_u) \\ &\leq 8\phi_{OPT}(X_u) + \phi(X_u) \end{align*}$$

This bound means that the expected potential after placing the first center is at most 8 times the optimal potential of all clusters plus their current potential before any centers are placed.

Obviously, this case is satisfied as it is not only reasonable but matches the inductive formula when $t=0$.

Base Case 2:

We have $t=u$ and $u=1$ since now we have placed a single center, which gives us the following:

$$\begin{align*} E[\phi'] &\leq \left(\phi(X_c) + 8\phi_{OPT}(X_u)\right) \cdot (1 + H_1) + \frac{1 - 1}{1} \cdot \phi(X_u) \\ &\leq \left(\phi(X_c) + 8\phi_{OPT}(X_u)\right) \cdot (1 + 1) + 0 \cdot \phi(X_u) \\ &\leq \left(\phi(X_c) + 8\phi_{OPT}(X_u)\right) \cdot 2 \\ &\leq 2\phi(X_c) + 16\phi_{OPT}(X_u) \end{align*}$$

In this case, we know from lemma 3.2 that $E[\phi'] \leq \phi(\mathcal{X}_c) + 8\phi_{OPT}(\mathcal{X}_u)$, which means this gives us the following:

$$\begin{align*} E[\phi'] &\leq 2\phi(X_c) + 8\phi_{OPT}(X_u) \end{align*}$$

which confirms that the actual expected potential is even better than what the inductive formula requires:

$$\begin{align*} E[\phi'] &\leq 2\phi(X_c) + 8\phi_{OPT}(X_u) \leq 2\phi(X_c) + 16\phi_{OPT}(X_u) \end{align*}$$

Inductive Step 1:

In this step, the authors show that the bound holds for both $(t-1, u)$ and $(t-1, u-1)$, which implies that $(t, u)$ also holds.

In the first case they consider choosing a center from a covered cluster, which happens with probability exactly:

$$P_{c} = \frac{\phi(\mathcal{X}_c)}{\phi} \text{ where } \phi = \phi(X_c) + \phi(X_u)$$

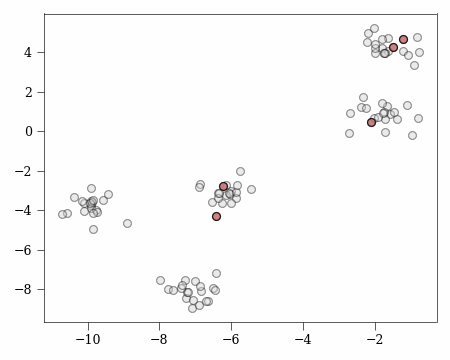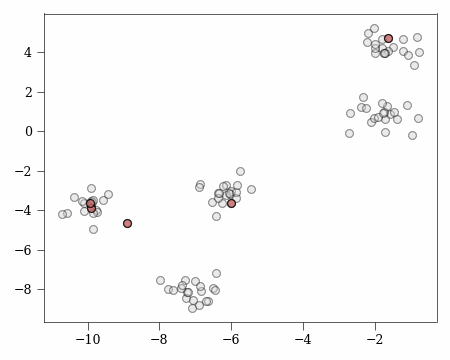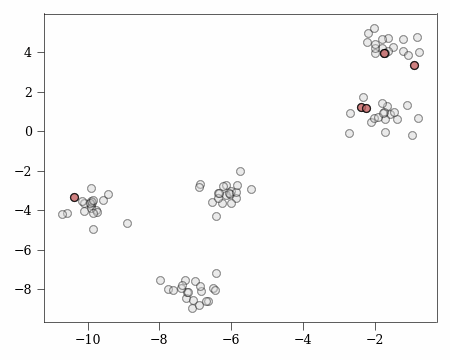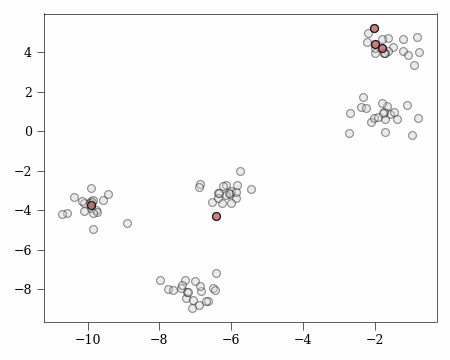
Now looking back at our working example, we first get our first center:

c1 = X[C_OPT == 0][0]

Then use this center to get the following cluster:

Now to calculate $\phi(\mathcal{X}_c)$, we can do so by computing the _phi (defined earlier) which is the potential for a single cluster:

phi_xc = _phi(X[C_OPT == c], c1)

which means for $\phi(\mathcal{X}_u)$ it is:

phi_xu = _phi(X[C_OPT != c], c1)

Giving us $P_{c}$ which is:

prob_c = phi_xc / (phi_xc + phi_xu)
print(prob_c)

0.0048291760708577755 

which makes $P_u = 1 - P_c \approx 0.995$.

We can clearly see from the visualisation what “covered” and “uncovered” clusters mean, and the probability of selecting from an already covered cluster is significantly lower than selecting from an uncovered cluster.

Returning to the general proof, if we pick from a covered cluster, three things happen:

1. No new clusters get covered
2. The number of uncovered clusters stays the same
3. We recursively have one fewer center to place

This means we apply the inductive hypothesis for $(t-1, u)$, and since adding centers to covered clusters can only improve the potential, the first case is guaranteed to satisfy the bound.

As a result, we have the following:

$$\begin{align*} E[\phi'] &\leq P_c \cdot \left(\left(\phi(X_c) + 8\phi_{OPT}(X_u)\right) \cdot (1 + H_{t-1}) + \frac{u - t + 1}{u} \cdot \phi(X_u)\right) \end{align*}$$

Inductive Step 2:

Now we look at the second case which is choosing a center from an uncovered cluster which the authors denote as $A$. This happens with probability:

$$P_A = \frac{\phi(A)}{\phi} \text{ where } \phi = \phi(X_c) + \phi(X_u)$$

Using our practical example, we can calculate the probability of choosing specific from the uncovered cluster $A$. We choose an uncovered cluster abitrarily:

u1 = X[C_OPT == 1][0]
u = C_OPT[np.argwhere(X == u1)[0][0]] 
A = X[C_OPT == u] 

where the following gives us the potential of the uncovered cluster $A$:

phi_A = _phi(X[C_OPT == u], c1)

we then also want the potential of the other unconvered clusters not in $A$:

phi_O = _phi(X[C_OPT == 2], c1)

then the probability of choosing $A$ is:

prob_A = phi_A / (phi_xc + (phi_A + phi_O))
print(prob_A)

0.8058971324477772

If we plot the result we find that the uncovered cluster $A$ is much more likely to be chosen than the other uncovered cluster $O$.

This matches our intuition of how $k$-means++ works since we are more likely to choose points that are further from any existing center.

Now looking back at the general proof, if we pick from an uncovered cluster, three things happen:

1. $A$ moves from $\mathcal{X}_u$ to $\mathcal{X}_c$
2. Uncovered clusters go from $u$ to $u-1$
3. We have $t-1$ centers to place

When choosing any point $a \in A$ with the conditional probability $p_a$, we have the following:

$$\begin{align*} E[\phi'] &\leq \left(\phi(X_c) + \phi_a + 8\phi_{OPT}(X_u - A)\right) \cdot (1 + H_{t-1}) + \frac{(u-1) - (t-1)}{u-1} \cdot \phi(X_u - A) \\ &\leq \left(\phi(X_c) + \phi_a + 8\phi_{OPT}(X_u - A)\right) \cdot (1 + H_{t-1}) + \frac{u-t}{u-1} \cdot \phi(X_u - A) \\ &\leq \left(\phi(X_c) + \phi_a + 8\phi_{OPT}(X_u) - 8\phi_{OPT}(A)\right) \cdot (1 + H_{t-1}) + \frac{u-t}{u-1} \cdot (\phi(X_u) - \phi(A)) \end{align*}$$

and by using lemma 3.2, we know that:

$$\sum_{a \in A} p_a \cdot \phi_a \leq 8\phi_{OPT}(A)$$

which means that we can replace $\phi_a$ with $8\phi_{OPT}(A)$ to get the following:

$$\begin{align*} E[\phi'] &\leq \left(\phi(X_c) + 8\phi_{OPT}(A) + 8\phi_{OPT}(X_u) - 8\phi_{OPT}(A)\right) \cdot (1 + H_{t-1}) + \frac{u-t}{u-1} \cdot (\phi(X_u) - \phi(A)) \\ &\leq \left(\phi(X_c) + 8\phi_{OPT}(X_u)\right) \cdot (1 + H_{t-1}) + \frac{u-t}{u-1} \cdot (\phi(X_u) - \phi(A)) \end{align*}$$

then the result including the probability of choosing $A$ is:

$$\begin{align*} E[\phi'] &\leq \frac{\phi(A)}{\phi} \cdot \left[\left(\phi(X_c) + 8\phi_{OPT}(X_u)\right) \cdot (1 + H_{t-1}) + \frac{u-t}{u-1} \cdot (\phi(X_u) - \phi(A))\right] \end{align*}$$

This derived result gives us the contribution of choosing from one specific uncovered cluster $A$, however, the algorithm itself doesn’t know which cluster it will choose from and therefore we need to account for all possible clusters.

Incomplete Still Working

TODO: finish lemma 3.3 and the rest of the proofs.